Les équations de Navier-Stokes sont traitées dans Castem2000 par l’opérateur ‘NS’. Cet opérateur discrétise les termes de diffusion et de convection, et nous l’utilisons dans le cas incompressible. Il reçoit en paramètres la viscosité cinématique Nu, et calcule l'incrément (ici, le champ des vitesses) pour une discrétisation en élément finis EFM1 par un algorithme explicite décentré.
Nous effectuons les calculs sur un maillage (Figure II.1) de forme trapézoïdale afin de " suggérer " au logiciel de rechercher une solution s’évasant légèrement avec l’altitude, comme nous l’attendons dans le cas d’un jet. Le maillage est plus " raffiné " au niveau de la sortie de la cheminée, où est introduit le fluide, puis " s’éclaircit " lorsque l’altitude (x) et la distance à l’axe (y) augmentent. Les éléments, de type " Qua8 ", sont des trapèzes définis en 9 points : les 4 sommets, les milieux des 4 arrêtes, et le centre de l’élément. Le parois latérales doivent être suffisamment éloignées de l’axe central pour supposer qu’elles n’influent pas sur le jet, sans toutefois trop augmenter la taille de la boite, donc le temps de calcul. En pratique, on les éloigne de 8 à 10 largeurs de la cheminée.
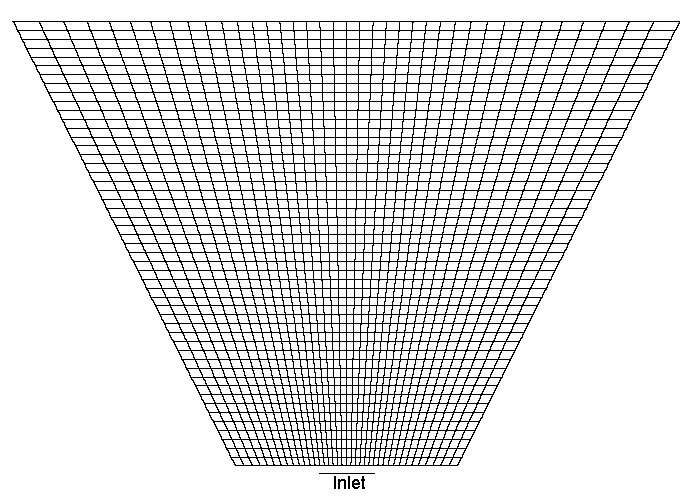
- Figure II.1 -
La modélisation de l’atmosphère libre, donc d’un espace semi-infini en x et infini en y où le fluide est au repos à l’infini dans toutes ces directions, n’est évidemment pas possible numériquement. Pour s’en approcher au mieux nous avons donc imposé les conditions aux limites suivantes au contour de notre maillage :
La condition d’adhérence impose une vitesse nulle au " sol ", c’est à dire en tous les points d’altitude nulle hors de la sortie de notre cheminée.
Au niveau de la sortie de la cheminée, on impose le profil de Poiseuille obtenu comme résultat de l’étude préliminaire : Ux parabolique, s’annulant aux bord de la cheminée, Uy nul.
Sur les autres parties du contour, nous avons utilisé l’option de Castem permettant de simuler une " contrainte nulle " (cf. code de calcul en Annexe).
Cela se traduit par :

(II.3)
Cette méthode nous semble apporter la meilleure solution, après avoir essayé en vain d’imposer une pression constante aux bords, ou une condition de glissement sur les parois latérales.