

| Convection libre: Le problème de Rayleigh Bénard |   |
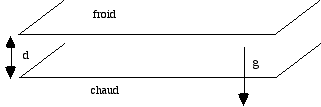
deux plaques limitant un fluide, une est plus chauffée que
l'autre.

rouleaux vus de côté (plaque en haut et en bas)
| Convection libre: Le
problème de Rayleigh
Bénard |
  |

figure dans
le cas où la surface est libre et où le fond est
chauffé:
on voit (en vue de dessus) des hexagones
| Le problème de Rayleigh Bénard, équations |   |
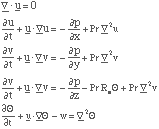
Il apparaît donc le nombre sans dimensions suivant en facteur du terme moteur:
Ra =α ΔT g Pr d 3 ν-2
Pour la température, elle est imposée:
Θ=0 sur z=0 et Θ=0 en z=1
| Le problème de Rayleigh Bénard, équations |   |
par élimination
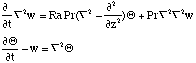
avec comme conditions:
w=0, ∂w/∂z=0, Θ=0sur z=0 et z=1
On cherche la solution sous forme de "modes propres" (au sens des vecteurs propres) :
(w,Θ) = (W(z),T(z)) eimx+ily est.
Les perturbations harmoniques introduites (en cos(mx+ly)) seront atténuées si Re(s)<0 ou au contraire amplifiées si Re(s)>0, Re désignant la partie réelle. Une subtilité de cette configuration est que l'on peut chercher un mode "marginalement stable" (s=0). D'où si k=÷(m2+l2):
(D2-k2)2W = k2 Ra T ; (D2-k2) T = -W;
soit (D2-k2)3T = -k2 Ra T ;
| relation de dispersion |   |
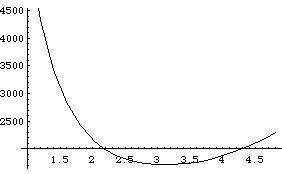
On obtient la courbe de stabilité marginale si dessous.
Ra
 k
k
figure Ra fonction de k
La valeur minimale est Rac~1707,76.
Le nombre d'onde critique est kc~3,1.
Bénard (Exemples de
résolution
numérique).