LA301
Mathematiques pour la physique
Cauchy
Le baron Augustin-Louis Cauchy (1789-1857):
(Né l'année de la revolution Francaise...)
"Il fut l'un des mathématiciens les plus prolifiques, derrière Leonhard Euler, avec près de 800 parutions et sept ouvrages ; sa recherche couvre l’ensemble des domaines mathématiques de l’époque. On lui doit notamment en analyse l’introduction des fonctions holomorphes et des critères de convergence des séries et des séries entières. Ses travaux sur les permutations furent précurseurs de la théorie des groupes. En optique, on lui doit des travaux sur la propagation des ondes électromagnétiques."
voir:
http://fr.wikipedia.org/wiki/Augustin_Louis_Cauchy
|

|
Outils pour la visualisation
Dans ces TD, j'utilise parfois le language de programation Matlab pour visualiser les fonctions, et la convergence des séries entières. Matlab est un programme payant, un peu cher, mais d'habitude les universités ont un certain nombre de licences. Voir le site de Matlab: http://www.mathworks.fr/products/matlab
Une alternative gratuite est le programme Octave, voir http://www.gnu.org/software/octave, qui est un clone de Matlab développé par la communauté des internautes codeurs...
Tous ce qui est fait avec Matlab ou Octave peut être fait avec d'autres languages comme fortran ou c, mais Matlab ou Octave sont des languages interprétés (sans compilation). On a accés aux variables de calcul de manière intéractive, il y a beaucoup de fonctions pour visualiser les variables: vecteurs , matrices... et il y a beaucoups de fonctions utiles et pratiques...
Vous trouverez ceci sur le site d'octave:
http://www.gnu.org/software/octave/about.html
"There were still some people who said that we should just be using Fortran instead, because it is the computer language of engineering, but every time we had tried that, the students spent far too much time trying to figure out why their Fortran code failed and not enough time learning about chemical engineering. We believed that with an interactive environment like Octave, most students would be able to pick up the basics quickly, and begin using it confidently in just a few hours."
Corrigé du devoir d'entrainement
Vous le trouverez ici:
 la301_de.pdf. la301_de.pdf.
Travaux dirigés
TD 2: Differentiabilité
 la301_td2.pdf. la301_td2.pdf.
TD 3: conditions de Cauchy et holomorphie.
 la301_td3.pdf. la301_td3.pdf.
Indications:
Exercice 1, question 1:
 la301_td3ex1q1.pdf. la301_td3ex1q1.pdf.
Exercice 3, question 2:
 la301_td3ex3q2.pdf. la301_td3ex3q2.pdf.
TD 4: Holomophie et convergence des séries
 la301_td4.pdf. la301_td4.pdf.
TD 5: Rayon de convergence des séries
 la301_td5.pdf. la301_td5.pdf.
TD 6: Intégrales dans le plan complexe.
 la301_td6.pdf. la301_td6.pdf.
TD 7 et 8: (semaine du lundi 6 octobre) Series de Taylor et de Laurent, Intégrales dans le plan complexe.
Vous trouverez tout dans le document pdf suivant:
 la301_td78.pdf [5 mégas]. la301_td78.pdf [5 mégas].
Une version plus légère mais moins claire (encore lisible...) est là:
 la301_td78_leger.pdf [300 kilos]. la301_td78_leger.pdf [300 kilos].
- Les exercices des TDs 7 et 8
- Representation des lignes de niveaux pour certaines fonctions des exercices
- Un code Matlab pour visualiser la convergence des series des exercices, comme par exemple la série géométrique
- La visualisation de cette convergence pour la série géométrique et certaines séries des exercices. On observe en particulier le rayon de convergence des séries: à l'intérieur de ce rayon, la série converge, et à l'extérieur, en général, elle tend vers l'infini...
Ici, je vous met quelques pages d'un livre de formules, pour la décomposition en élément simples, et pour un résumé rapide des propriétés des functions de la variable complexe:
 la301_formulaire.pdf la301_formulaire.pdf
Ici, La correction des exercices manquant des TD 7 et 8. En plus de ça, vous trouverez les graphs de la convergence des séries de Taylor et de Laurent correspondant à la série géométrique, à l'intérieur et à l'extérieur du cercle unitaire:
 la301_td78_plus.pdf la301_td78_plus.pdf
TD 13, équations différentielles
Ici, un petit formulaire des procédures pour résoudre quelques types communs d'équations différentielles:
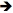 la301_equadif.pdf la301_equadif.pdf
Ici la correction des equations de Bernoulli et de Ricatti du td 13:
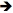 la301_bernoulli_ricatti.pdf la301_bernoulli_ricatti.pdf
TD 17, systèmes différentiels
Le TD 17 et sa correction:
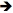 la301_td17.pdf la301_td17.pdf
Ici un petit example de modes propres pour un problème de physique: l'évolution de la temperature sur une plaque plane. La temperature est imposée à zero aux bords (conditions de Dirichlet homogène), et la température dans le domaine satisfait une dynamique harmonique: la dérivée temporelle de la température est égale aux laplacien de la température. Vous verrez sur l'image, les 100 premiers modes propres (de haut en bas et de gauche à droite...)
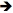 la301_lap.jpg la301_lap.jpg
Contexte
A l'époque de Cauchy, les nombres complexes n'étaient pas très utilisés en dehors des calculs de racines des polynômes (depuis le 16ième siècle). Il cherche à étendre aux nombres complexes la théorie des fonctions. Comme les fonctions de la variable complexe peuvent être assimilées à des fonctions sur R2, la dérivée dépend de la manière dont on approche le point auquel la dérivée nous intéresse. Pour palier à ce problème, et ainsi pouvoir définir la dérivée sans considérer la fonction comme une fonction sur R2, il impose les fameuses "conditions de Cauchy". Les fonctions qui satisfont ces conditions pourront donc être manipulées de la même manière que les fonctions réelles, ces fonctions seront appelées les fonctions "holomorphes" (ou de "forme entière").
Il s'est avéré que les fonctions holomorphes, en plus de permettre une généralisation de toute l'analyse des fonctions réelles, ont des propriétés très intéressantes: leurs parties réelles et parties imaginaires sont harmoniques, c'est à dire satisfont les équations de Laplace. L'équation de Laplace est à la base des équations aux dérivées partielles de la physique: équation de la chaleur, équation des ondes, équation d'Euler pour les fluides parfaits, équation de Stokes pour les fluides sans inertie... En partant de fonctions simples holomorphes, on peut construire des solutions générales et démontrer des propriétés de ces solutions (existance et unicité par example).
Depuis les principes fondamentaux de la mécanique par Newton, c'est la plus grande avancée du processus de mathématisation de sciences, et en particulier de la mécanique. La théorie des fonctions complexes de Cauchy est à la base des méthodes classiques de résolution des problèmes en mécanique des fluides et des solides. On peut donc dire que c'est à cause de (ou grâce à?) Cauchy que la mécanique Française est principalement tournée vers une approche mathématique. Les mécaniciens anglo-saxons de leur côté, ont attendu la révolution industrielle pour inventer toutes les méthodes dont ils ont eu besoin sur le terrain, pour résoudre par exemple les problèmes de machines à vapeur.
De cette manière, on peut penser à une opposition des méthodes dans les "maths pour la physique": une approche "à la française", des mathématiques vers la physique, et une approche "à l'anglaise", de la physique vers les mathématiques.
|